This is a guest post by Anastasiia Pusenkova, Quantum Application Lead at Nord Quantique
Quantum computing has seen explosive growth in recent years, offering phenomenal potential across multiple industries such as pharmaceuticals, logistics, energy and cryptography, to name a few. One of quantum’s most promising applications is simulation of materials, where advanced algorithms combined with error-corrected hardware could soon transform the entire industry.
Classically Intractable tasks
Classical computational methods i have driven scientific progress for decades, particularly in computational chemistry. However, computational demands increase significantly for larger molecules, making classical methods insufficient as they struggle with the exponential growth in the complexity of these calculations, and the resources required. This makes accurate simulations close to impossible for large chemical systems such as complex proteins, large biomolecules and advanced materials.
In the rapidly evolving field of quantum chemistry, quantum algorithms could revolutionize molecular simulations and computational chemistry. These algorithms leverage the principles of quantum mechanics to efficiently simulate molecular systems, potentially outperforming classical methods by exploiting quantum parallelism and superposition.
While no quantum algorithm has yet surpassed the performance of advanced classical methods in solving practical real-world problems, the theoretical capability of quantum computing to outshine classical methods is widely acknowledged. And many in the quantum industry are currently working towards this objective.
Glossary of useful terms:
Gates: In quantum computing, gates are basic operations similar to logic gates in classical computing that execute during each "clock cycle" or unit of time.
Circuit depth refers to the minimum number of these gates that need to be applied sequentially in order to successfully run a given algorithm.
Noise is essentially interference from electromagnetic fields and other elements around quantum computers which causes random errors in quantum computations, imposing a limit on the circuit depth that can be run with an acceptably low error probability.
NISQ Era and Useful Use Cases
The quantum industry is currently in the Noisy Intermediate-Scale Quantum (NISQ) era, characterized by quantum computers with up to about a thousand physical qubits. Quantum systems at this scale may indeed outperform classical computing for certain tasks, but they are constrained by significant noise levels within the systems themselves. Consequently, the range of practical use cases for these NISQ quantum systems is restricted, preventing us from fully demonstrating their potential.
Yet despite these limitations, NISQ devices have shown promising initial results in specialized applications where quantum advantages could be effectively utilized, highlighting their potential for more efficient problem-solving compared to classical computers.
One exciting application is quantum chemistry, where NISQ devices have been used to simulate small molecules such as H2, LiH, BeH2 and others. These early successes pave the way for more complex simulations that could be a huge step forward for materials science.
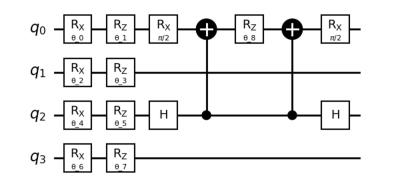
To illustrate this, below is an example of a quantum circuit used for simulating the hydrogen molecule (H₂) on a NISQ device ii.
This circuit showcases the quantum gates and operations involved in the simulation of a simple molecule. However, for larger and more complex molecules, the quantum circuits become significantly more intricate. This complexity arises from the need for a greater number of qubits and gates, as well as more complex qubit interactions. While it appears feasible to simulate initially classically intractable molecules in the NISQ era, achieving “chemical accuracy” poses numerous technical challenges.
This task demands exceptionally high-quality gates and the integration of sophisticated error correction mechanisms. Furthermore, the estimated runtime for a single calculation on a NISQ machine may span months or even years, compounded by the nature of quantum calculations, which prohibit the checking or saving of intermediate results.
To address these challenges and fulfill Feynman’s vision of simulating quantum processes with quantum systems, both hardware improvements and the development of more efficient algorithms are imperative. These requirements define the motivation behind Nord Quantique's recently announced collaborative effort with OTI Lumionics, initiated in 2024.
Quantum Material Discovery
The appeal of quantum simulations for materials discovery lies in their cost-effectiveness and rapid material screening capabilities, promising to minimize waste and accelerate discoveries. Nord Quantique’s project with OTI aims to develop a "Materials Discovery Platform," a quantum computing system for high-accuracy simulations of advanced materials, in particular simulating properties for OLEDs and other semiconductor applications. At the core of this initiative is a collaboration between Nord Quantique's error-corrected superconducting qubits and OTI's Qubit Coupled Cluster algorithm, allowing for very efficient use of quantum resources, and enabling precise simulations of advanced materials. This partnership maximizes the advantages of our current quantum hardware, by generating the shallowest circuit depth possible as well as reducing the number of gates and qubits required, making them less sensitive to noise, and creating more favorable conditions to execute calculations. Our focus is to use this algorithm on an early fault-tolerant processor that includes initial error correction, to assess its performance and optimize future fault-tolerant implementations.
This partnership therefore has the potential to unlock new capabilities for quantum computers when optimized for error-corrected systems.
How Many Qubits and Gates Are Actually Needed?
The effectiveness of quantum computing depends on the number of qubits and their quality. Ensuring low error rates and implementation of quantum error correction (QEC) are crucial for achieving reliable results.
Most quantum computing methods require a large overhead of additional physical qubits to support the logical qubits which perform calculations. When there is an error in an individual physical qubit, other qubits from the overhead are used to preserve the logical information so the calculation can continue without being corrupted by the error. Error correction is therefore achieved by using these additional physical qubits to detect and correct errors, ensuring the accuracy of the computations.
Today, most quantum computers typically contain anywhere from tens to hundreds of qubits in total. But practical applications, such as materials simulations, may require thousands of high-fidelity logical qubits. As an example, for drug discovery the estimated number of logical qubits required is 1000, therefore a quantum circuit would have to be run with more than 1 billion gates iii to carry out this operation. If we consider the overhead which can require up to 1000x physical qubits as a redundancy for error correction to preserve the logical information in one logical qubit, we must build a quantum computer with at least a million qubits to see the first relevant results in this field. Another challenge is the high quality of quantum gates required for precise calculations in quantum chemistry.
A different approach may solve the problem
Our team began its work by developing error correction protocols using a single bosonic qubit. Recent findings highlight their approach's success, achieving a significant 24% reduction in errors on a single qubit without the need for a large overhead of additional qubits dedicated to error correction iv . As a result, a single physical qubit could directly serve as an error-corrected logical qubit, thus drastically reducing the amount of qubits required for error correction to only a handful. Additionally, Nord Quantique's superconducting platform operates at a clock rate in the MHz range, significantly enhancing computational speed, which is crucial for any practical quantum algorithms. This positions it as one of the fastest options among alternative technologies.
Furthermore, our collaboration with OTI Lumionics will be exploring the development of a hybrid mode (digital and analog) for quantum processing units to leverage the bosonic nature of our hardware. The addition of this “analog mode” simplifies the simulation of multi-level quantum systems – a task that becomes exponentially complicated when mapping onto the two-level qubit systems.
In both endeavors, we are targeting the creation of a hardware-efficient simulation platform tailored for quantum chemistry simulations, by having only a handful of qubits dedicated to error correction. This makes it potentially suitable not only for the NISQ era but also lays the groundwork for low-overhead fault-tolerant quantum computing — an ambitious goal that promises to reshape the landscape of quantum computation.
Perspectives and transition to Fault-Tolerant Quantum Computing
Rigorous benchmarking and validation are essential for building confidence in quantum computing for practical applications. This involves comparing the performance of quantum algorithms on quantum hardware against classical simulations to ensure accuracy, particularly in fields like materials science.
That said, having a one-to-one ratio between a bosonic physical qubit and an error-corrected logical qubit may still not be enough to reach early fault-tolerance, which requires error per operations as low as 1e-9 to 1e-12. In this context, concatenation with qubit codes to transition toward fully scalable FTQC might be required, and the bosonic nature of Nord Quantique’s qubits would drastically cut down the required resources.
Progress in the NISQ era and advances in Quantum Error Correction open the door for quantum simulations which can drive significant advancements in materials science. Collaborative efforts like the one we’ve started with OTI demonstrate dedication to unlocking quantum computing's potential, making the goal of accurately simulating complex materials more attainable as we advance towards fully error-corrected quantum computers.
___________________________
(i) Such as Density Functional Theory and wave function methods ranging from the simplest Hartree-Fock approach to more advanced configuration interaction methods
(ii) Ilya G. Ryabinkin, Tzu-Ching Yen, Scott N. Genin, & Artur F. Izmaylov. (2018). Qubit coupled-cluster method: A systematic approach to quantum chemistry on a quantum computer.
(iii) Fault-tolerant quantum computing will deliver the transformative promise of quantum computing (Part-I)
(iv) Dany Lachance-Quirion, Marc-Antoine Lemonde, Jean Olivier Simoneau, Lucas St-Jean, Pascal Lemieux, Sara Turcotte, Wyatt Wright, Amélie Lacroix, Joëlle Fréchette-Viens, Ross Shillito, Florian Hopfmueller, Maxime Tremblay, Nicholas E. Frattini, Julien Camirand Lemyre, & Philippe St-Jean. (2023). Autonomous quantum error correction of Gottesman-Kitaev-Preskill states.